728x90
반응형
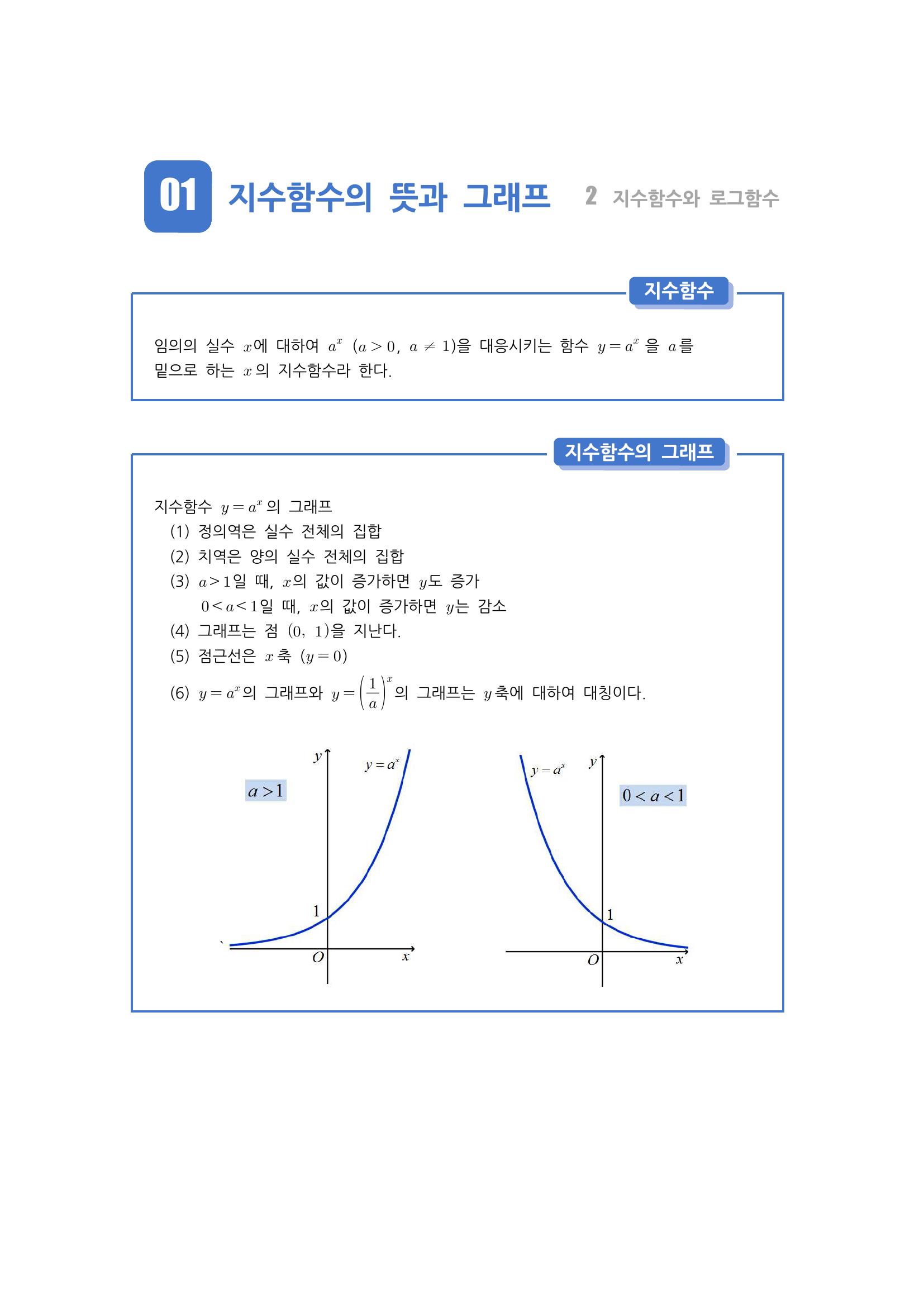
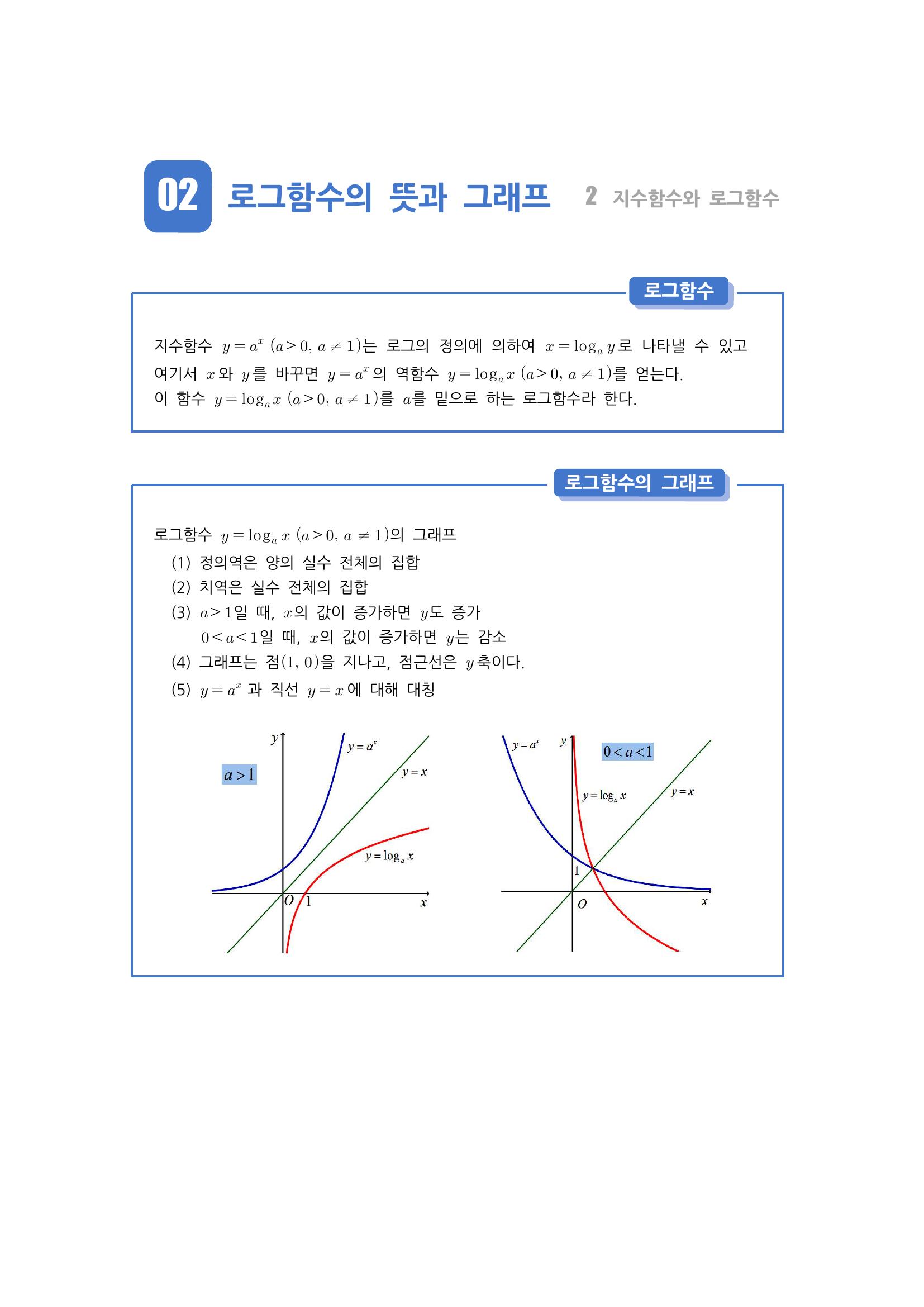
지수함수와 로그함수는 서로 역함수 관계입니다.
역함수를 그래프(기하적)로 해석하면 y=x 대칭입니다.
또한 역함수 관계끼리의 함수가 서로 만나는 점, 즉, 교점은 대게 y=x 위에 존재하게 됩니다.
f(x)가 지수함수이고 g(x)가 로그함수이고 서로가 역함수 관계일 때, f(g(x))와 g(f(x))는 무엇일까요?
우선 고1의 역함수를 배울 때, 역함수끼리의 합성함수는 x가 된다는 것을 배웠었죠. 기억하시나요.
f(g(x))=g(f(x))=x라고 배웠었죠.
하지만 로그함수와 지수함수는 조금 다릅니다.
왜냐하면 서로 정의역이 다르기 때문이죠.
f(x)가 지수함수이고 g(x)가 로그함수라면
g(f(x))의 정의역은 모든 실수입니다. 즉, f(g(x))=x라는 것이 성립합니다.
반면, f(g(x))라면 로그함수가 먼저 대응되므로 정의역이 x>0가 되므로
f(g(x))=x (x>0)라는 함수입니다.
전혀 다른 함수가 된다는 의미입니다.


하루하루 목표를 위한 거름이 되길 바랍니다~
728x90
반응형
'📝수학📝 > 수학1,수학2,미적분' 카테고리의 다른 글
| 고차방정식, 연립이차방정식, 삼차방정식과 사차방정식의 풀이, 연립이차방정식의 풀이 (0) | 2022.03.31 |
|---|---|
| 이차방정식, 판별식, 이차방적식의 근과 계수와의 관계, 이차방정식의 인수분해, 이차방정식의 켤레근, 이차방정식의 실근의 부호 (0) | 2022.03.31 |
| 항등식, 나머지 정리, 미정계수법(계수비교법, 수치대입법), 인수정리, 인수분해 공식^^ (0) | 2022.03.31 |
| 다항식의 정리, 다항식의 덧셈과 뺄셈, 지수법칙, 다항식의 곱셈, 곱셈 공식, 조립제법 ^^ (0) | 2022.03.31 |
| 수열의 수렴과 발산 ^^ (0) | 2022.03.31 |




댓글